Development of the contactees net.
As we said before, Sesma (picture) received, in 1967, masses of reports and read them loudly in his
club. They were describing the everyday's life on this strange planet, the
habits of its inhabitants, their social behaviour, their political
organisation and their history. All that was mixed with information about
the propulsion of their machines, the way of travelling over many light
years, biology, their theory of evolution, and even their metaphysics.
(picture) received, in 1967, masses of reports and read them loudly in his
club. They were describing the everyday's life on this strange planet, the
habits of its inhabitants, their social behaviour, their political
organisation and their history. All that was mixed with information about
the propulsion of their machines, the way of travelling over many light
years, biology, their theory of evolution, and even their metaphysics.
The Ummits indicated to Sesma that they were not typing the texts
themselves, but were helped by a stenotypist, paid by them, and living in
the Spanish capital. He was mailing the letters to different persons, to
addresses given by his unconventional "employers".
In the fifties, the Ummits took contact with the Earth, in circumstances
we will describe later because they are very funny. They would have then
traveled all over the Earth, in different countries ( including the United
States, of course). After becoming familiar to our languages, they wished
to communicate with us, first by phone, then through writings, which was
less dangerous for them. To do so, a group located in Australia, near the
town of Adelaide, would have modify a terrestrial type-writer machine to
be able to command it by voice.
The Ummits are very clumsy, as they admitted shameless. As one of them
wanted to drive a car, in Australia, he had an accident and died, they
said. You may ask how these lubberly people could have develop such a
technology on their planet. That has not been reached in one day.
We already mentioned that they are hemeralopic, living
essentially during the night. The day, they simply sleep, like owls.
At the beginning of their history, they would have live in burrows, like
rabbits. After, they would have build a complex underground architecture.
On UMMO, the visible buildings, constructed on the floor, have essentially
industrial or scientific functions.
As they arrive on Earth, what we will describe precisely
later, they choose quite rapidly a semi-wild region, to avoid being
discovered too fast. They found a little hill near the small town of Digne,
situated in south of France. Naively, seeing all this constructions they
thought to have landed near a scientific complex. They said to have been
very amazed as they discovered that people were just living in these
constructions.
One must read, in this report called "the first days on Earth",
the anxiousness of these people, getting in touch with our floor,
expecting immediate attack from Earth's inhabitants, rushing out from
underground habitations.
The Ummits say to have built contacts with lots of other
extraterrestrial groups. We may deduce that this way of living, like
moles, is usual and that we may represent an exception on this point. We
will see later why.
The texts give numerous details, sometimes flavourful, about the History
of this hypothetical planet UMMO. Along their History they would have, as
we did, developed a technology. At the beginning these people would have
used their hands. But once day, came the invention where the use of manual
capabilities was no longer necessary. Our technologies, with the emergence
of informatics and robotics, converge in that direction. We also have
voice controlled machines. Our robots become, slowly, intelligent 11.
The Ummits' technology is situated at the horizon of
ours. The first age of technology was pure mechanics. We learned building
tolls, to hew stones, to sew clothes. Second step, with the invention of
fire we developped chemistry. We transformed the food, we hardened the
points of our arrows. Then we discovered metals and energy sources. We
find oxydo-reduction, created alloys and learned to melt pieces and to
forge them.
Third step: the nuclear. We only are at the beginning on this point. But
it is evident that in some centuries, if we do not have crashed ourselves
with our rotten bombs, we will develop production systems of unlimited
energy, non polluting 12.
The Ummits would have reached this stadium since centuries. They
also have no more pollution problems as they became masters in the art of
nuclear transmutation. They know how to transform their wastes in neutral
matters like helium.
They also say to have no problem in becoming raw materials. When they want
to build a machine with such or such atoms, they do not look for them in
nature, but would build them using the stones on the roads or the nitrogen
of the atmosphere.
The Ummits possess, of course, computers, with a power which compared to
ours, would look like abacus compared to a Cray-2. A set of computers
would manage the whole planet, not only the production chains, but also
the social net. This society reached, after an History, as muchturbulent
as our, a perfect social stability.
In short, the Ummits would no more work. As playing tennis or golf would
never occur to their mind, they no more have the use of their hands.
They also say that they have no real vocal strings, but quite primitive
pharyngeal structures (what would give us a very nasal voice on the phone).
This phonation organ would disappeared at puberty for most of the
individuals 13. They would then be fitted with an amplification system
constituted of two elements. The first, so big as a pea, would be
implanted by surgery under the tongue, for all their life. The second
would pick up the signal emitted by the first and would produce audible
sounds. They would wear it hanged on their neck as a necklace.
By the way, they would transcode the weak sounds emitted by their organ in
two ways. The deep sounds would be amplified to hold a conversation. The
higher sounds would be changed in ultra.sounds, and would control their
machines.
So, when a Ummits speaks with deep tons, he discusses with another Ummits.
If they go higher in frequency, they speak to their computers or vacuum
cleaner.
As they no more used their hands, the Ummits would have
changed them into sensitive organs, through genetic manipulations.
Our skin is plastered of cells which are sensitive to infrared. This is
not of use, except to avoid, at the last moment to be burned by a fire.
For the Ummits, being with night habits, the infrared perception was at
the beginning mostly important, like olfaction. They would have then
developed it artificially and could, with the help of the skin on their
hands, see pictures, more fuzzy than the one of the retina, but still
reliable.
Corollary: their skin would be so sensitive, too
sensitive so that they could not make some manipulations, as for instance
pushing the button of an elevator. They would use therefore their
"nodes of fingers", they mean the articulations.
That would explain why the Ummits would have equipped a
writing machine with a voice control system, what could have produced a
mess. Effectively, detected by the secret services on this country, they
had, according to the texts, to leave their hotel room in a rush and have
hidden their devices in a laundry basket, that happily no one discovered.
They would have pick them back afterwards, with great fear.
A spy must take with him as less gadgets as possible,
which could revealed his identity. A good killer kill with a kitchen knife
or an electric cable, it's well-known.
The Ummits who came on Earth would be chosen beyond
those who have a phonation organ not too degenerated. Whether the presence
of sound emitter, on their clothes would be noticed. In general they avoid
to carry hi-tech alien technology.
After this incident, the members of the expedition would
have estimated that it would be more secure to hire the services of a
stenotypist, more than hanging around with writing machines, equipped with
system from another planet (some terrestrial machines would have been
taken back on UMMO and modified).
They would then have some secretaries, in different countries, paid by
them.
Landing of a Ummit vehicle at San José de Valdeiras,
near by Madrid, in 1967.
The Spanish secretary sent lots of letters to different
persons since months, as one of his "boss", called DEI 98,
dictated him a letter about the arrival of three vessels on Earth. One of
them should land near Madrid, some days later. The man posted the letter
to several persons,a s asked by the guy.
Sesma and now half a dozen people received this mail.
The landing area was not indicated with precision "for security
reasons". The Ummits just gave a approximation of the latitude and
longitude and some time indications.
Some contactees waited for the event at
home. Some others, more enthusiastic, went on site with cameras, in case of a UFO
sighting.
None of them could take photos of the vessel, which landed anyway in the
suburb of Madrid, in San José moreover Valdeiras, as reported by the
witness of this landing. The vehicles let large tracks on the floor which
have been photographed.
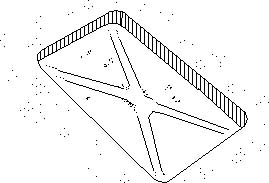
Figure 7. One of the traces left on
the floor by the vessel, at San José moreover Valdeiras, photographied by
Rafael Farriols and Antonio Ribera 14.
The press has been informed of this affair, which made the first page of
all newspapers. Thirty years later, the landing of San José de Valdeiras
is still discussed, like all UFO cases are discussed. Let's say it was the
landing of an unidentified object with traces on the floor.
The feelings of the Ummits' secretary.
As he saw all this story, the secretary went into
panic.
Till now, he did not ask himself lots of questions about his employers.
They were paying him very generously, and, in this time of unemployment,
that was worth. But, having sent a letter announcing the arrival of a UFO,
which really came scared him.
With a terrible fear, he sent, without revealing his
identity, a letter to all the people to whom he sent the reports of the
previous months.
This letter is quite amusing. The day before the landing
of this "cosmic vehicle" (which would have simply picked up to
members of the expedition: sir DEI 98 and miss YU 2, to bring them back
home), the Ummits would have ask him to house them.
What they would have accepted. The story is here
flavourful. Half a dozen Ummits would be arrived, at dawn. The wife of the
secretary, had prepared a meal that the visitors refused, says the letter.
They would have slept on the floor on some sort of foam, deposited with a
spray, which would have evaporated in the morning 15.
The stenotypist and his wife would not have close an eye
during the whole night. Through the window of the lounge, a Ummit, dumb
like a fish would have sent little balls which would have flown in the
neighbourhood's streets.
- Some monitoring devices, moving with
MHD, would
have explained on of the member of the group to their hosts.
This landing affair also destabilised the group of
"the happy whale". Esoterism, yes, real flying saucers which
land, this was no more acceptable at all !
In the mean time, the group became
larger. Beyond its
member were now the engineer named Villagrassa and the writer and
journalist Antonio Ribera  (picture
down left). He was the perfect copy of Grouch Marx and had once written to
the American actor, reproaching him to use his image to make money.
Groucho, amused, answered him very kindly.
(picture
down left). He was the perfect copy of Grouch Marx and had once written to
the American actor, reproaching him to use his image to make money.
Groucho, amused, answered him very kindly.
One day when the radio announced that a saucer had
landed at San José de Valdeiras, Rafael Farriols (picture down) was in
his car, not far from there with his wife Carmela. Naturally curious, he
went on the site and found the engineer Villagrassa, completely
disappointed with many cameras hanging on his neck.

- I knew they would come ...
- You knew what ? asked Farriols (pictured above).
Villagrassa told him the whole story that Farriols found
very amusing, so that he decided to join the group of "the happy
Whale", which was very shocked. Rafael wanted to know more and try
baught the documents owned by Sesma. As he was very rich (he was the
director of a Plexiglas factory in Barcelona) he was ready to give a big
amount of money for this acquisition.
But Sesma got rid of his whole documents for a
ridiculous sum, as if they were burning his fingers and ceased to showe
any interest for this UMMO affair, preferring to limit his contacts with
"Martians" and "Venusians".
Ribera gave a copy of all letters he personally received to a priest, the
father Guerrero, a fanatic esoterist. As the news of the landing came to
the public, the religious man became completely mad and began to speak to
all journalist he met.
The newspapers said in this occasion:
- An extraterrestrian colony is living in an
underground cave, in the Sierra of Gredos, nearby Madrid.
The Ummits went into panic and left Spain immediatly. If
father Guerrero would not have revealed every thing the whole story would
have kept the confidentiality wanted by the authors of the letters till
the beginning. The landing affair would have been one more case in the
swamp of UFO cases.
Believing the texts received by the Spanish several
years later, the group of contactees in Spain would be a group beyond ten
others dispatched all over the world. They would be particularly some in
France, Germany, Italy, Australia, Russia, Canada, Zimbabwe, Denmark and
of course the United-States.
The Ummits would have ask all theses contactees to be very discrete, or
they would stop sending information, and their disciples would have obeyed
their orders. The Spaniards received at the same period a letter from a
Canadian contactees :
- Why do you have chatted about all that ? You
perfectly know we have the instruction to keep quiet.
But they give no names or addresses. The Ummits say in
the reports which came to the Spaniards long after the affair of San José
moreover Valdeiras that they started a large disinformation, what we are
used to now. One of their agents, or one of them, would have given to the
press a camera film with very clear pictures of the vessel, flying in the
suburb of the town, and which have been largely reproduced in the
newspapers and in book related to UFOs.
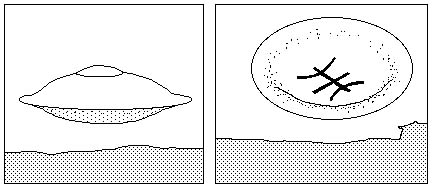
Figure 8. The Ummits vessel as they were appearing on the photographs
transmitted by an unknown person to the Spanish press.
The Ummits sign may be seen on the bottom side.
The group of Madrid and the group of Barcelona.
The human behaviour, facing such affair, is interesting,
everyone finally, looking through with a different eyet. For a man like
father Guerrero, reading these sheet produced a real mystic delirium.
Sesma preferred to keep on with other dreams, less real and then less
distressing. The Ummits, after a moment of worry, asked themselves whether
they would keep on or not the Spanish experiment.
After many days, they found it to be a good way of
studding how the public could react to some information about their
existence and about the UFO problem in general. Contrarily to their
worries, the affair went rapidly down and disappeared in the background
noise of the Ufologist.
They began their mailings again. Beyond the addressees
was now included Rafael Farriols, who would become the archivist of the
case. This was a equilibrated man, with a solid sense of humour. Around
him was constituted the group of Barcelona. In the members, a certain
Barranechea, an old communist, and Farriols secretary Hiltrud Franz, whose
nickname was Lou.
In Madrid where members of the first hours, Jordàn
Peña, psychologist, the engineer Domingez and the physician Auguire. The
affair went slowly during years. The reports kept on coming and Rafael was
archiving them very precociously. I had contact with the affair at this
period.
I became the friend of Ribeira and Farriols, I met the others at different
occasions.
Pena(picture) was a strange and secret man. Domingez (engineer and
electronician) and Aguire (physician) were believing to be elected. It
looks like two clubs, distant geographically, which were meeting from time
to time, to bring information in common. We will come back on the story of
these nets afterward and on what happened to each of them.
Who is at the origin of Ummits reports ?
I (Mr.Petit) am writing these lines in 1995. The first
documents have been received in Spain in 1966. This affair lasts since 29
years. Personally, I paid some interest, and also took an active part in
it, since 20 years.
Who is hidden behind this fabulous story ? A group of funny scientists ?
The intelligence services of some powerful country ? Or really
extraterrestrians in flesh and bones ? Interesting question.
Let's discuss the first hypothesis. The one of a crazy
scientist, unique author of all these text, is not credible, because the
reports touch too different domains. Overall, the whole information is
self-consistent. The different reports are connected one to the other. It
seems to have a very strong underground logic.
This means that an interdisciplinary group should have
been constituted with several crazy scientists, very tenacious, to have
kept on this experiment during so much time 16. With which goal ? To be
amused by some Spaniards, unable to understand a line of these texts ?
This makes no sense. On the other side, as these texts are scientifically
very productive, I can't imagine some scientist making such gifts.
The given indications, for instance in cosmology, were
quite precise. They involved me in building an original model concerning
the twin structure and the evolution of the Universe, which is something.
These scientific works are not inconsistent deliriums, whether I could not
have published them in high level revues, which have the reputation to be
very cautious. Their implications are important. We will come back on them
later. We explain, beyond other things, the large structure of the
Universe and the origin of the spiral shape of galaxies. Our last work (
see the appendix ) identifies the matter of the twin Universe to the
cosmological anti-matter. This building fits perfectly the informations
presented in the Sesma book, in 1967. This anti-matter is enantiomorphic
and owns an opposite time arrow.
A student in science could not have produce the keys
concerning a new cosmological solution. In case of a "funny
scientist", he would have to build this solution, achieve the work,
in a relatively precise way.
Let me give you an analogy. The equation of general
relativity are so complex, from a mathematical point of view, that it is
impossible to give indications by just writing anything, by hazard. This
is equivalent of give the first five numbers of a safe combinaison which
would have seven numbers. If by manipulating the lock of the safe after
many tries and efforts the door would open, this means that the one who
gave the fisrt five numbers knew the complete combinaison. If the author
would have given them by hazard, the safe could not have been opened. If
one or several scientists are at the origin of the key-information, they
would have already build the whole basic theory, very complex. In this
case, why haven't they published immediately this work? In the scientific
world, people do not make such gift, of such an importance.
This remark is also true for the hypothesis of a
manipulation by some secret services. Some have given this explanation,
involving ... the KGB, with the goal of "destabilising Spain and
prepare the period after Franco". This is absurd for two reasons:
- The mailing of document continued after Franco's death
( I have received my last letter a week ago ).
- The falling down of USSR and the disorganisation of the KGB, in 1990,
did not slow down the arrival of document and the funny telephone calls.
Some also pretend I am the author of these texts. Let me
tell you at this point a funny story. Just after the publication of this
book in France, where I decided to reveal the source of my works, a
mathematician in Lyon wrote me these lines:
Dear sir,
The president of the University gave me your book,
saying it was fascinating most of his students. He asked me, as I know
general relativity quite well, to make a severe critic of it. I then read
the scientific aappendix where your scientific publications are reproduced,
and analysed them. I could not find any errors. These work are of great
quality, and I want to congratulate you to have invented all this story
about extraterrestrians to get the attention of people on this work.
Best regards.
This does not fit the hypothesis where I would have been the author of
these texts. Effectively, they have been written in 1967, at a period when
I was still a simple student. Sesma published most of them in a book the
same year, under the title "UMMO, otra planeta habitado", which
means " UMMO another inhabited planet"17.
If this mathematician of Lyon was right, I should have,
as I was a simple student, to cosign all these key-scientific informations
in a book written in a language I do not speak, and to published this work
telling myself " I will use that in twenty five years, when I will be
scientist ..."
What remains ? The hypothesis of an extraterrestrial
origin of course. I know this may sound vertiginous, but it is eventually
the most logical one
Other aspects of the UMMO affair.
The UMMO affair is not only a gathering of reports
received by postage, or notes taken during calls. There exist reals
anecdotic facts. Rafael Farriols owns, for instance, a magnetic tape of
the voice of these persons. The affair goes back to the end of the sixties.
One night, a man was driving on the road between Barcelona and Madrid. He
was the signing clerk of the Rothschild bank institute. Suddenly, on the
road's side what did he saw ? A saucer with some man beside it. Very
helpful, he stopped, thinking "may be he has a breakdown" In
such peculiar situations, the head of people are often having very
ridiculous thoughts.
The man had a fully normal appearance, and was speaking
in Spanish, pretending he was originated from earth, and that his
ancestors have been kidnapped on a planet far away.
- But, asked the banker, you never thought of escaping ?
- Not at all. When I see what happens here, this does not incite me to
come back.
Both went their way. The madridelenian went back home,
driving normally, calmly, after having quitted the pilot of the saucer. At
home, his wife was waiting for him. He told him the story. Suddenly he had
terrible nervous shocking, and had a strong psychological break-down,
began to cry, as if he was living all this emotional charge afterwards. He
spoke about his adventure around him.
The press reported this affair, but this was a UFO story
beyond lots of other. At this time, this type of happening where very
usual on Earth. Some days after the diffusion of the news on radio, he got
a phone call from a man with the voice of Donald duck. The man questioned
him on his adventure and said frankly:
- We also are extraterrestrians, travelling on Earth,
but we do not know this other ethnic group. We would like to meet you to
discuss about that.
They took an appointment. In between, the protagonist of this story had
been in contact with the group of Madrid. They all said:
- These are the Ummits ! This is their voices.
The day of the appointment, the flat was full. All were
handing a list of questions they wished to ask to the travellers of the
planet UMMO. Rafael Farriols was also there. Good technician, he equipped
by hazard the phone with a mike connected to a tape. When you hear the
tape they recorded this day, you can first hear the voice of the Spaniard,
who tells his story with passion. Then the phone rings. He took the
headphone, and said more slowly: Here they are.
Farriols recorded then a monotonic voice, nasal, which says.
- Que sus hermanos reunidos en su domicilio no
formulen preguntas. Suplicamos perdon, senor, disconecto la communication.
Translation :
- The people joined in your flat should not ask any
questions. Please excuse us, sir, I cut the communication.
This sentence is repeated three times.
Of course, any joker could have done that, pinching his
nose. In the seventies, Antonio Ribera gave me a copy of the recording,
and I let it analysed in the laboratory for phonetics of my University, in
Aix-en-Provence. From these short message has been made a sonogram. In the
abscissa, horizontally, the time. Vertically the frequency. It is the way
of analysing voices or sounds, human parole or bird singing.
The specialist in charge on this analysis told me:
- This is not a human voice. Look at the frequencies,
they are quite stable in time. We call it "recto tono". The
frequency spectrum is quite flexible, and a man can't keep stable
frequencies when he pronounces vowels. Here, this constancy is very
remarkable.
The person who made these sounds has a relatively rigid pharynx. Or may be
it is a human voice transcoded by a "vocoder".
I don't think vocoder were existing at the time when this voice has been
recorded. Let's add, that the frequency spectrum was matching with the
information given by the Ummits about their quite primitive phonation
organ. The UMMO affair is full of such peculiar details ( and I will tell
about all of them in this book). Let's speak now about some other aspects.
In one of the reports, the authors speak about a phone
conversation they had with a certain Theodore T. Polk, in Pittsburgh. He
asked him why they call our planet OYAGAA, what they were translating
"planet of the square". Next, a part of their reports, devoted
to this affair.
- We knew the existence of your planet by receiving a radio emission,
in 1949 (Earth time). We knew afterwards, that it had been emitted during
some short communication try, from a trawler based at Bergen, in Norway.
The message took fifteen years before reaching UMMO, distant of fifteen
light years from Earth. It was emitted in 1934. By increasing the
frequency of your radio emitters, the electromagnetic waves could then
cross the gas layers of the Earth atmosphere. On UMMO we have big antennas
flying in orbit around our planet. The received message was short : few
ten seconds. Immediately, we admitted it was coming from intelligent
beings, what surprised us a lot, as usually, life is not appearing around
stars like your sun, with a gaseous envelope of a temperature of about six
thousands degrees. Our sun Iumma, is colder: five thousand five hundred
degrees only, and this is a general condition for all the inhabited planet
we know.
Immediately we decided to send a first mission in direction of your
planetary system. We tried without success to decipher your message, which
was the alternation of long and short signals. At the end, one of us
suggested that you tried to send us a theorem on the square. This is the
reason why we call your planet the "planet of the square", which
has evidently no thing to do with the real content of the message, as we
understood years later. But the name stayed.
Reading these lines, I had the idea to localise Polk, in
the United-States. This was not so easy, but I succeeded, thanks to friend
living in Chicago. He was no more living in Pittsburgh, but in a suburb
called Export. I called him on the phone.
- Hello mister Polk ?
- Himself.
- Mister Theodore T. Polk ?
- Yes it's me.
- My call will surprise you, no doubts. I am a French scientist and I call
you to ask you if you did not received some phone calls, in the sixties,
of people pretending to come from another planet ?
- What a funny idea !?!
- Let's change the question, have you received at this period calls from
persons who had some difficulties to speak, with duck-voices ?
- No.
This looked like a false trail. The author of the
document may had chosen this name by hazard. There must be a lot of Polk
in Pittsburgh, given the large number of people living their, who have
polish origins. I asked by hazard a last question:
- Does the planet of the square has some meaning for
you ?
Polk lowered his voice and said:
- Yes, but I prefer not to speak about that on the
phone.
I tried several times, through mails, to know more, but
this was Polk who asked me questions, to which I answered. I told me
simply that after this affair, he received lots of calls similar to mine,
coming from different parts of the world, including Japan.
As I wanted to know more on the phone, he slept away:
- I thought a lot of time about writing you a letter,
but I think this could have dramatic implications.
I could not know more. Polk, quite old, is dead today
and took his secret with him. May be I fingered one of the member of the
American net.
Other anecdotes refers to news items. The Ummits says,
for instance, that after living two years in their refuge near Digne, they
moved first toward Marseille, on the southern French coast, where I could
not found their traces again, and went in different countries, Spain,
Germany, and Australia. In each of these country, they say to have built
quite large underground refuges. The one of the Sierra moreover Gredos, in
Spain, could, believing them, house seventy people, when the one of Digne
may receive only six and would measure four meters over height.
Apparently, their head-quarter would have been implanted in an underground
base in Germany.
They would have thought less dangerous to fade into the population of
large towns than to multiply the number of in and outgoing from their
underground bases. So, as they wanted to settle in Spain, they would just
have hired a room in the house of a woman, Doña Margarita Ruiz moreover
Lihory, living in Albacete. This woman, who had been of the mistress of
Franco, was belonging to the Spanish high-society. They have got her
sympathy by curing some real diseases and other which were "imaginaries",
by presenting themselves as Sweden physicians.
These Sweden would have then occupied, in her home,
going out only night for security reasons. They would have arranged a
laboratory in her cellar where they would have done biological experiments
on animals ( at the beginning they thought about opening a veterinary
hospital).
All that would have been perfect if the daughter of Doña Margarita had
not done something they would not have foreseen and that had heavy
consequences. She would have stolen the key of the room and would have
inspected it during their absence.
The Ummits say that they were studying, at this time,
some virus brought from their planet, which were not dangerous for the
humans (because they consider to be human beings,
even if they are genetically incompatible with us).
One the viral source brought from their planet would have become very
aggressive to the human and the daughter of Doña Margarita would have
contracted an infection. As she had plunged her arm in a tank and rubbed
her eye, this infection would have damaged her hand and her ocular globe.
The Ummits would have been astound by this unforeseen consequences 18.
They would have been in different places that this young girl has
frequented, could have localised the infected people and cure them with
the help of pulsed ultra-sounds, by making exploding on distance the
envelopes of the viruses. But it would have been impossible to cure this
way the young girl, whose state became very serious. The situation would
have been so serious the the Ummits living in Germany, and particularly
the so-called YU-2, chief of the earth expeditionaries, would have
converged toward Albacete to have a crisis meeting.
The Ummits would have estimated that to cure the young
girl could in the end reveal their presence on Earth and would have
decided to let her die. As doctors, they would have signed the "permission
to dispose of the body ". Till this point, these facts are verified.
The daughter of Doña Margarita deceased effectively in mysterious
circumstances. The Ummits then decided, prudently, to cut away the
infected body parts, namely the hand and the eye. But someone noticed that
the corpse had been mutilated and the police began to investigate. The
Ummits went away, and Doña Margarita was jailed and found guilty. The
affair made a big noise in the Spanish town, as she was accused of having
done some guilty practices on the body of her own daughter. She was
finally disculpated, but died from sorrows some times later.
At this time the boy-friend of Dona Margharita daughter felt from a window
and died. In the Ummits texts we learned that he would have entered the
underground local and would have recuperated some devices there. The
secret services of different countries, beyond these the CIA 19, were
crawling in the region and would have taken contact with the young man. He
would have uncarrefully tried to sell them the devices. He would have been
then assassinated.
Secret services, CIA, murder, is all that just a gathering of news items
divers, well exploited ?
In the eighties, we went to visit Rafael Farriols, in his splendid
hacienda situated on a hill, near the town of Argentona, not far from
Barcelona. He had accepted to let us photocopy hundred of pages, what we
did. On the way back home, as I was driving, my friend Jean-Jacques
Pastor, who was my interpreter in this affair (Although from Spanish
origin, I am not speaking this language), read with avidity this new crop
of information. Suddenly he had a surprise exclamation:
- Oh ! Rafael forgot in this bundle of sheets a
report coming from a private detective he would have paid to inquire on
this affair of the cut hand of Albacete.
- So what !?
- There are some letters following. Apparently, Rafael has not told him
really on what he was inquiring. The man says to have investigated on site,
the house of Doña Margarita already have be destructed. But he found many
things by asking the neighbourhood. For example, as the house has been
destructed, an underground laboratory has been found. It seems that there
were large tanks with some animals body parts. There was even a horse-head
!
- And then ?
- In the next letters, the detective says he used the contacts he had with
the policemen of the city and tried to know more (detective are often
ancient policemen). He confirms the presence of secret services during the
affair, and the suspicious death of the boy-friend of the young lady.
- And ? ....
- The file ends with a last letter where he writes to Farriols : "I
heard so many extraordinary things that I prefer to coming to you and tell
them by word of mouth "
next part
ufo-conatcts english language
main



